Windows95 激活
/ 4 min read
早期的系统及软件激活大部分使用了离线激活技术,究其原因是因为当时的网络并不发达,许多软件都不具备离线激活的条件。故许多软件和系统厂商采用离线激活码的形式来验证软件的合法性。
离线密钥验证的原理其实非常简单,即对一整段输入的内容进行某种形式的计算和排列组合,最终得到一个合法的结果,程序即判定为激活完成。
以遭到破解的Windows95安装过程中的激活程序为例,其零售版激活程序要求输入长度为10位数字的激活码,格式为:
xxx-xxxxxxx
后来人们发现,000-0000000 和 000-1111111 等极为简单和重复的密码也能成功通过验证。经过对激活程序的反编译,有人成功破解出了 Windows95 激活程序的运行逻辑:
在零售版中,连字符前的三位数字采用黑名单制,即除了黑名单上列出的几种组合,其余任何内容均可通过测试,如下图:
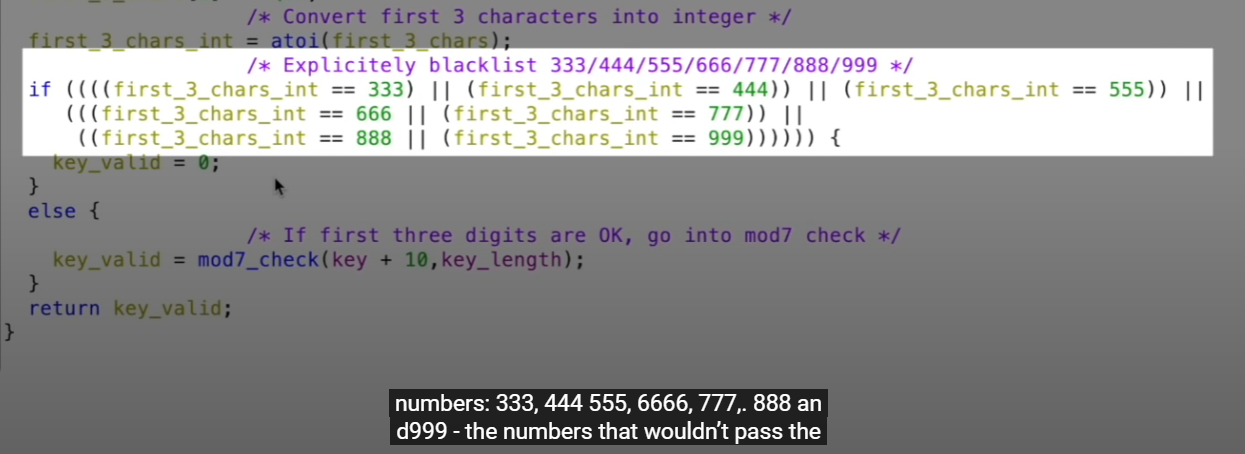
黑名单给出的几种排列组合
余下的七位数字则会将各个数位的数字求和,并验证其与7的整除性。若Sum能被7整除(不留余数),程序即判定为序列号有效,验证通过。
以激活码000-1111111为例,前三位000未出现在黑名单中,验证通过。后七位1111111相加各数位相加之和等于7,可被数字7整除。到此为止,整个程序的流程验证完毕。
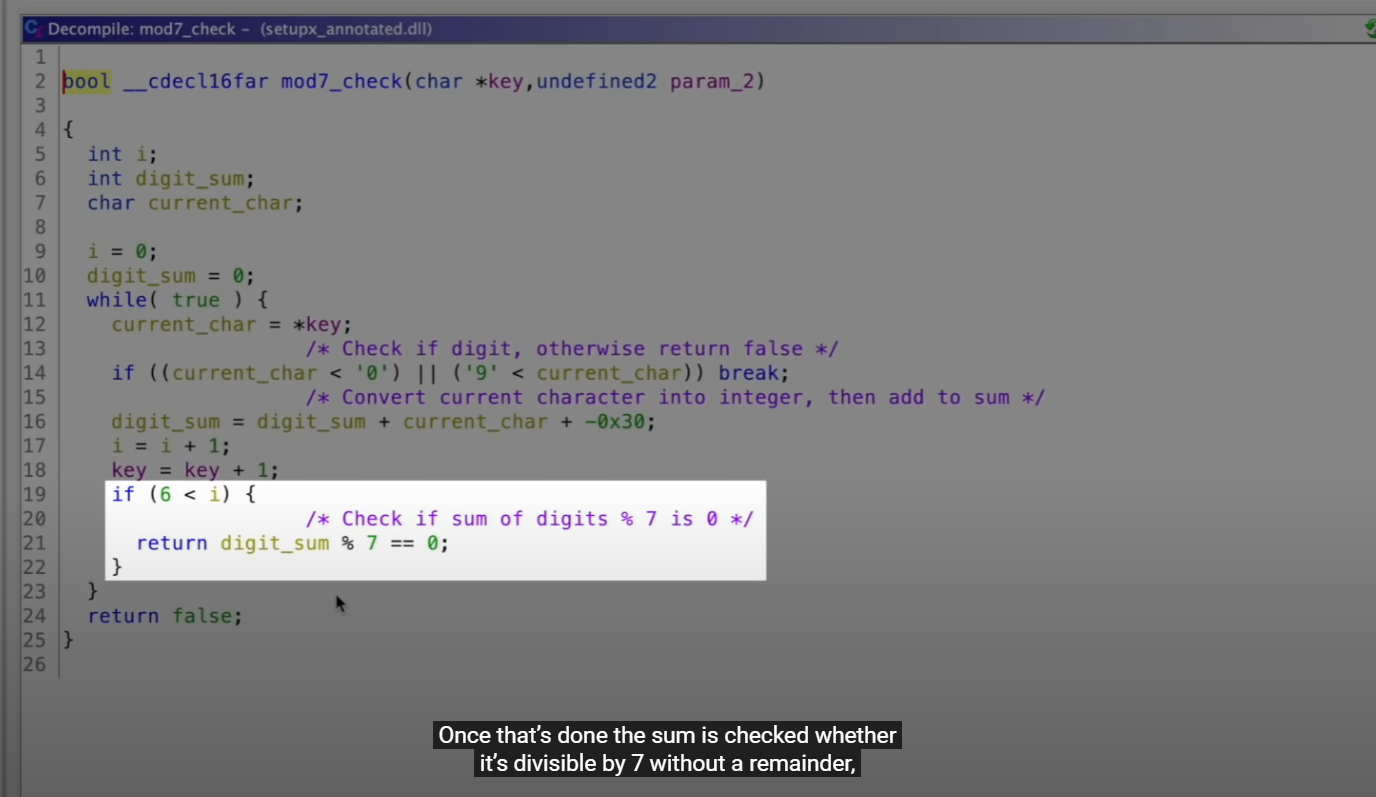

111-1111111通过验证的原理
除零售版外,OEM的激活码有所不同,但也被民间大神成功反编译:

与零售版相同,OEM版的激活码也由几个部分组成。其中前两个数字需满足为1-366之间的数字;第四、五位数字则为95-03之间的数字。中间由OEM作为OEM激活码的识别标志。下一段则为与零售版相同的mod7整除测试。最后五位数字不设限制,填写任意五位数字均可通过验证。
以下为 Windows 95 OEM 密钥测试程序
undefined2 __stdcall16far check_oem_key(char *key,int len)
{ int key_length; int is_oem; int first_3_digits_int; int second_2_digits_int; undefined2 check_result; int i; int i_; char first_three_digits [4]; char second_two_digits [3]; char kc;
key_length = LSTRLEN(key); if ((((key_length == 0x17) && (key[5] == '-')) && (key[9] == '-')) && ((key[0x11] == '-' && (is_oem = check_oem_str(3,0x11704f9d,key + 6,len), is_oem == 0)))) { /* Check first 5 digits, must be numeric */ i = 0; do { kc = key[i]; if (kc < '0') { return 0; } if ('9' < kc) { return 0; } i = i + 1; } while (i < 5); /* */ copy_partial(3,key,len,first_three_digits); first_three_digits[3] = '\0'; first_3_digits_int = atoi(first_three_digits); if ((first_3_digits_int != 0) && (first_3_digits_int < 367 /* check if between 1 and 366 */)) { copy_partial(2,key + 3,len,second_two_digits); second_two_digits[2] = '\0'; second_2_digits_int = atoi(second_two_digits); if (((second_2_digits_int < 3) || (94 < second_2_digits_int)) && (((key[10] == '0' && ('0' < key[0x10])) && (key[0x10] < '8')))) { i_ = 0x12; while ((kc = key[i_], '/' < kc && (kc < ':'))) { i_ = i_ + 1; if (0x16 < i_) { /* jump to part after oem- */ check_result = mod7_check(key + 10,len); return check_result; } } } } } return 0;}代码源地址:https://gist.github.com/nezza/a25bee13f25a1733a4c7a1d3d1cf5882
文章部分插图来源:Youtube:stacksmashing